1. Úvod do jazyka Python

Tato přednáška přestavuje stručný úvod do programovacího jazyka Python. Probrány jsou jak základní tak pokročilejší nástroje, které budou používány po zbytek kurzu. Pro zájemce o hlubší porozumění Pythonu doporučuji kurz Vědecké programování v Pythonu (12PYTH), ze kterého tato přednáška čerpá.

Další užitečný kurz v češtině je například od Pyladies.

1.1. Instalace Pythonu a prostředí Jupyter notebook

V druhé části kurzu Numerických metod budeme používat moderní prostědí Jupyter notebook (soubory s koncovkou .ipynb), které jsou velmi vhodné jak na výuku tak na rychlé otestování a prototipování kódu.

Máte volbu mezi dvěmi možnostmi, jak sledovat přednášku a mít možnost spouštět kód:

1. Pracovat v online interaktivním prostředí - Binder, JupiterHub FJFI, Google Colab

2. Pracovat lokálně na svém počítači

1.1.1. Postup instalace

Online interaktivní prostředí (doporučuji)

Pro spuštení interaktivní verze této stránky klikněte ve vrchním menu na a zvolte:

• Binder - ve kterém lze Jupyter notebook (JP) upravovat a následně uložit na disk

• JupyterHub - místní prostědí běžící u nás na FJFI, umožňuje uložit ve vlastním účtu

• Google Colab - na vlastní nebezpečí

Pozor

Spuštění prostředí Binder může trvat několik desítek sekund. Jupyter notebook je v tomto prostředí uložen pod dočasným URL. Při zavření okna se postup ztratí! Je nutné tedy upravený soubor před zavřením okna stáhnout.

Lokální prostření

Pro programování na svém počítači je třeba:

1. Nainstalovat Python (často již nainstalován s OS)

2. Nainstalovat Jupyter notebook

3. Stáhnout repozitář z GitHubu (ve vrchním menu tlačítko )

4. Pak příkazem > jupyter notebook se spustí prostědí v prohlížeči.

Jako alternativu doporučuji použít IDE (Integrated Development Environment) Visual Studio Code, ve kterém je možné přidat rozšíření pro Python a Jupyter notebook. Také je možné přímo stáhnout GitHub repozitáře přes odpovídající rozšíření.

Tip

Další možnosti instalace nástrojů jsou popsány zde.

Pro pokročilé možnosti virtuálních prostředí postupujte podle postupu zde nebo zde.

1.2. Jupyter notebook

Jupyter notebook je interaktivní dokument obsahující buňky se spustitelným kódem, textem, obrázky, vzorci a apod. Je to velmi vhodný nástroj pro výuku a proto všechen materiál k tomuto cvičení je ve formě těchto notebooků.

V této kapitolce se krátce seznámíme, jak se s Jupyter notebooky pracuje. Podrobný popis všech vychytávek si můžete přečíst zde.

1.2.1. Hello world!

Úkol

Napište print("Hello world!") a stiskněte Shift + Enter (nebo Ctrl + Enter)

print("Hello world!")

Hello world!

Pomocí klávesy b vložíte další řádek do JP.

• Stiskněte b.

Odstranění řádku: vyberte řádek v JP a stiskněte d + d

Klávesou a vložíte nový řádek nad právě vybraný.

Přidání buňky s textem:

1. Stiskněte a.

2. Vyberte tento nový řádek a stiskněte m. Nyní lze do řádku místo kódu zapisovat text.

Pokud chcete řádek převést na kód, stiskněte y.

Tip

Pro nápovědu možných funkcí stiskněte Tab.

Pro zobrazení dokumentace k vybrané funkci stiskněte Shift+Tab.

1.3. Jazyk Python

Python je univerzální programovací jazyk, hojně používaný vědeckou komunitou. Existuje spousta knihoven řešící celou řadou úloh za vás. Některé nejpoužívanější knihovny si v tomto kurzu ukážeme.

Základní vlastnosti Pythonu (vs C++):

• Dynamicky typovaný jazyk - typ proměnné se určuje až při běhu programu

• Silně typovaný (strongly typed) jazyk - vše má jasně definovaný typed

• Interpretovaný jazyk - kód v Pythonu není kompilován, až při běhu dochází k jeho interpretaci

• Obsahuje rozsáhlou vestavěnou knihovnu modulů a funkcí

• Přehledná, jednoduchá a čitelná syntaxe

• Objekově orientovaný + funkcionální programování

1.3.1. Komentáře

Jednořádkový komentář se zadává za znak #, více řádků lze zakomentovat obklopením """:

# toto je komentar
"""
Komentar
na vice
radku...
"""
print("Hello world!") 
#print("Hello world not printed!") 

Hello world!

1.3.2. Základní aritmetické operace

Inicializace proměnných a, b, základní aritmetické operace a výpis výsledku pomocí funkce print():

a = 43
b = 5

soucet = a + b
rozdil = a - b
soucin = a * b
podil = a / b
podil_beze_zbytku = a // b

mocnina = a**b    # v C++ pow()
zbytek_po_deleni = a % b

# vypis
print('Součet ', soucet)
print('Rozdíl ', rozdil)
print('Součin ', soucin)
print('Podíl ', podil)
print('Podíl beze zbytku ', podil_beze_zbytku)

print('Mocnina ', mocnina)
print('Zbytek po dělení ', zbytek_po_deleni)

Součet  48.0
Rozdíl  38.0
Součin  215.0
Podíl  8.6
Podíl beze zbytku  8.0
Mocnina  147008443.0
Zbytek po dělení  3.0

1.3.3. Podmínky - if, else a elif

Za klíčovými slovy if a else musíme psát :.

cislo = 0

if cislo > 0:
    print(cislo, "je kladne.")
elif (cislo < 0):    # logický výraz může být uzavřen závorky
    print(cislo, "je zaporne")
else:
    print("musi to byt nula")

print("Tento text se vypise vzdy.")

musi to byt nula
Tento text se vypise vzdy.

Pozor

Vnitřní bloky kódu se v Pythonu odsazují o tab nebo čtyři mezery! (V C++ je block uzavřen závorky { a }, a odsazení může být libovolné.)

Logické hodnoty jsou True a False, operátory pro složitější logické výrazy jsou or, and a not.

x = 4
print(x > 1 and x < 3, x == 3 or x == 4)

print(True == (not False))

False True
True

1.3.4. Základní datové struktury

String (řetězec)

a = 3 * ("Abc%i" % 3) + "!"    # string lze vytvořit například takto
print(a)

Abc3Abc3Abc3!

# různé způsoby tisku čísla a textu
cislo = 37

print("cislo =", cislo)
print("cislo = " + str(cislo))
print("cislo = %i" % cislo)
print(f"cislo = {cislo}, cislo^2 = {cislo**2}")
print("cislo = {0}, cislo^2 = {1}".format(cislo, cislo**2))

cislo = 37
cislo = 37
cislo = 37, cislo^2 = 1369
cislo = 37, cislo^2 = 1369

Konverze typů

Každá proměnná má v Pythonu jasně definovaný typ.

x = 4
print(x, type(x))

s = "text"
print(s, type(s)) 

4 <class 'int'>
text <class 'str'>

Mezi datovými typy je možné přecházet pomocí speciálních funkcí:

int("3")        # string -> int
float("3.14")   # string -> float
str(3.14)       # float -> string

'3.14'

1.3.5. Kontejnery

Kontejnery jsou datové struktury obsahující větší počet prvků. Mezi základní patří:

• tuple - neměnitelný (immutable) seznam

• list - měnitelný (mutable) seznam

• dics - asociativní pole

• set - množina prvků

Dále uvidíme, že:

• Prvky nemusejí být stejného typu!

• Pro indexování (přístup k jednotlivým prvkům) se používají závorky [] a indexuje se od 0.

Tuple

Tuple je n-tice prvků, které po vytvoření nelze měnit!

tuple1 = (1, 'a', 5)           # Základní syntax vytváření tuple (kulaté závorky)
tuple2 = 1, 'a'                # Závorky nejsou povinné, ale... !
tuple3 = tuple(["a", "b"])     # Pokročilé: Vytvoření tuple z jiného kontejneru
tuple4 = tuple(range(0, 10))   # Pokročilé: Vytvoření tuple z iterátoru / generátoru
tuple5 = ()                    # Prázdný tuple
tuple6 = ("single", )          # Tuple s jedním prvkem
tuple7 = 0, "1", (0, 1, 2)     # Tuple může pochopitelně obsahovat další tuple

print(f"tuple1={tuple1}")
print(f"tuple2={tuple2}")
print(f"tuple3={tuple3}")
print(f"tuple4={tuple4}")
print(f"tuple5={tuple5}")
print(f"tuple6={tuple6}")
print(f"tuple7={tuple7}")

tuple1=(1, 'a', 5)
tuple2=(1, 'a')
tuple3=('a', 'b')
tuple4=(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
tuple5=()
tuple6=('single',)
tuple7=(0, '1', (0, 1, 2))

print(tuple4[0])         # První prvek
print(tuple4[-1])        # Poslední prvek
print(tuple4[-2])        # Předposlední prvek

0
9
8

Vyzkoušejte, že skutečně není možné přepsat prvky tuple:

#tuple1[0] = 58

V praxi se s tímto typem setkáte při volání funkcí, které vrací více hodnot. Odpovídající proměnné je pak možné rozbalit následujícím způsobem:

def dvecisla():
    return 37, 58

a, b = dvecisla()   # rozbalení tuplu
print(a, b)

37 58

List

List je opět n-tice prvků, ale oproti tuple je možné prvky měnit. Odpovídá polím (array) v C++. Navíc ale může obsahovat prvky různých typů!

list(), []                 # prázdný list
list1 = ["a", "b", "c"]    # list vytvoříme pomocí [...]
list2 = [0, 0.0, "0.0"]    # můžeme tam dát libovolné typy
list3 = list(tuple1)       # nebo list vytvořit z tuple

print(list1)
print(list2)
print(list3)

['a', 'b', 'c']
[0, 0.0, '0.0']
[1, 'a', 5]

Jazyk Python poskytuje tyto základní operace pro práci se seznamy:

# všechny dostupné funkce pro operace s polem
", ".join(item for item in dir(list) if not item.startswith("_"))

'append, clear, copy, count, extend, index, insert, pop, remove, reverse, sort'

list1.append("d")         # přidání prvku
print(list1)              # list1 se změnil!
list1.sort(reverse=True)
print(list1)
print(list1.pop())        # vyjme poslední prvek
print(list1)

list1.remove("d")         # odstranění prvku(ů)
print(list1)

['a', 'b', 'c', 'd']
['d', 'c', 'b', 'a']
a
['d', 'c', 'b']
['c', 'b']

U kontejnerů typu tuple a list lze provádět výběr více prvků najednou pomocí řezů podle pravidla:

[[dolní_mez] : [horní_mez] : [krok]]

l = list(range(10))

print(l[:])     # vyber všechny prvky
print(l[0:2])   # vyber první 2 prvky
print(l[:5])    # vyber prvních 5 prvků
print(l[1:7])   # vyber prvky 1-6
print(l[5:])    # vyber všechny prvky od indexu 5 dál 
print(l[-3:])   # poslední tři prvky

print(l[::2])   # sudé prvky

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1]
[0, 1, 2, 3, 4]
[1, 2, 3, 4, 5, 6]
[5, 6, 7, 8, 9]
[7, 8, 9]
[0, 2, 4, 6, 8]

Dict a Set

Tyto kontejnery používat typicky v kurzu nebudeme. Zájemci se o nich můžou vzdělat opět zde.

1.3.6. Opakování - cykly

For

Zde využijeme funkci range(min,max,krok), která vytvoří sekvenci celých čísel od min po max (prvek max není v sekvenci obsažen) s uvedeným krokem. Výchozí hodnoty jsou min = 0 a krok = 1. Tuto funkci lze použít několika různými způsoby:

print(list(range(10)))
print(list(range(0, 10)))
print(list(range(0, 10, 1)))

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

for i in range(10):
    print(i)

0
1
2
3
4
5
6
7
8
9

pole = [1,2,4,8,16]    # procházení pole verze 1
for i in range(len(pole)):
    print(pole[i])

1
2
4
8
16

Foreach

Další způsob procházení pole je pomocí foreach konstrukce, která v Pythonu má stejný zápis:

pole = [1,2,4,8,16]    # procházení pole verze 2
for x in pole:
    print(x)

1
2
4
8
16

While

Dalším typem cyklu je while cyklus, který běží dokud je splněna určitá podmínka.

x = 0
while x < 10:
  print(x)
  x = x + 1

0
1
2
3
4
5
6
7
8
9

Tip

x = x + 1 je možné napsat zkratkou pomocí x += 1 (ovšem C++ operátor x++ v Pythonu použít nelze!).

Continue

Pomocí příkazu continue lze přeskočit zbytek iterace v cyklu a skočit na další:

a = 0
while a < 5:
    a += 1
    if a % 2 == 0:    # sudá čísla nebudeme vypisovat
        continue
    print("a = %i" % a)
else:
    a = 1
print("Konec, a = %i" % a)

a = 1
a = 3
a = 5
Konec, a = 1

Break

Pomocí příkazu break lze předčasně ukončit cyklus:

# pomocí break najdeme největší trojciferené číslo dělitelné 19ti
a = 999
while a > 0:
    if a % 19 == 0:
        print("Výsledek je: %i" % a)
        break
    a -= 1
else:
    # break nespustí else část
    print("Nic jsme nenašli")

Výsledek je: 988

Poznámka

V Pythonu je možné psát else blok za while cyklus, který se spustí ve chvíli, kdy je podmínka False.

1.3.7. Definice vlastní funkce

Vlastní funkce se definují pomocí hesla def. Ukážeme si to na výpočtu faktoriálu pomocí rekurze:

def factorial(n):
    if (n < 2):
        return n
    return n*factorial(n-1)

factorial(10)

3628800

1.3.8. Další základní funkce

Python obsahuje několik základních funkcí, které se běžně při psaní kódu používají. Celý jejich seznam můžete nalézt zde. Tady je výtah těch nejběžnějších, které se nám budou hodit:

• dir() - vrací seznam dostupných funkcí

• print() - výpis na standartní výstup

• len() - vrací délku řetězce

• range() - vrací sekvenci/pole po sobě jdoucích čísel

• input() - čtení standartního vstupu

• str() - převod proměnné (čísla) na řetězec (string)

• int() - převod řetezce na celé číslo

• float() - převod řetezce na desetinné číslo

• type() - vrací typ proměnné

• open() - otevření souboru

• close() - zavření souboru

Úkol

Vyžádejte si od uživatele číslo pomocí funkce input() a vytiskněte jeho druhou mocninu.

Tip

Budete potřebovat také funkci int() nebo float().

cislo = int(input("Zadej cislo: "))
print(cislo**2)

100

1.3.9. Import knihoven

Pro využití určité knihovny v kódu je třeba danou knihovnu importovat. Například knihovnu pro různé matematické funkce přidáme pomocí import math (v C++ ekvivalentní #include <math.h>).

import math    # chceme načíst vestavěný modul math

print(math.sin(math.pi / 4))    # použijeme funkci sin a konstantu pi

0.7071067811865476

Využívání knihovny je možné usnadnit specifikováním, které funkce (proměnné) chceme importovat:

from math import sin, pi    # import pouze některých položek

print(sin(pi / 4))

0.7071067811865476

Nebo můžeme místo jména knihovny zadefinovat alias:

import math as m

print(m.sin(m.pi / 4))

0.7071067811865476

m.factorial(10)    # volání funkce faktorial z knihovny math

3628800

1.4. Knihovna numpy

NumPy je základní Python knihovna pro práci s numerickými daty, konkrétně s 1- až n-rozměrnými maticemi. Implementace je z velké části napsána v C a Fortranu a používá BLAS knihovny. Numpy tak umožňuje pracovat s numerickými daty ve stylu Python kontejnerů (existují samozřejmě rozdíly) a zároveň zachovat rychlost kompilovaných jazyků.

Poznámka

Numerické knihovny implementovány v rychlém jazyce (C, Fortran) pomocí optimalizovaných a odladěných algoritmů. Proto používání již implementovaných funkcí není jen pohodlnější, ale vede na významně rychlejší kód!

Je dobrá praxe snažit se vyhnout používání cyklů tam, kde lze využít některou z knihovních funkcí (jednoduchý příklad - násobení dvou polí po prvcích).

V této kapitolce se načíte:

• Jak pracovat s poli a maticemi v knihovně numpy.

• Jak provádět různé algebraické operace.

• Jak efektivně pracovat s daty pomocí různých triků.

import numpy as np  # import knihovny numpy

Tip

Pro nápovědu možných funkcí v knihovně numpy stiskněte Tab po napsaní np..

Pro zobrazení dokumentace k vybrané funkci klikněte na funkci a stiskněte Ctrl nebo Shift+Tab (Ctrl+Space vs VS Code).

Úkol

Vyzkoušejte si používání nápovědy a dokumentace. Najděte funkci, která vrátí diagonální matici s posloupoností čísel (1, 2, 3) na diagonále.

Co dělá funkce np.diagonal()?

A = np.diag([1,2,3])
print(A, np.diagonal(A))

[[1 0 0]
 [0 2 0]
 [0 0 3]] [1 2 3]

Funkce np.diagonal() vrátí prvky na diagonále 2D matice jako 1D pole.

1.4.1. Numpy array

Vytváření pole (obdoba list) je v knihovně numpy možné několika způsoby:

• Z již existujícího kontejneru (list nebo tuple).

• Pomocí knihovní funkce, která pole vygeneruje podle daného pravidla (arange(), ndarray(), zeros, …).

• Načtením ze souboru.

vector = np.array([1, 2, 3, 4])
vector

array([1, 2, 3, 4])

matrix = np.array([[1, 2], [3, 4]])
matrix

array([[1, 2],
       [3, 4]])

Proměnné vector a matrix jsou stejného typu (ndarray), ale liší se rozměrem - shape.

print(type(vector), type(matrix))

print(vector.shape, matrix.shape)
print(np.shape(vector), np.shape(matrix))  # druhá možnost

<class 'numpy.ndarray'> <class 'numpy.ndarray'>
(4,) (2, 2)
(4,) (2, 2)

Celkový počet prvků lze získat pomocí size, zatímco dimenze pole pomocí ndim:

print("size: %i" % vector.size, "dim: %i" % vector.ndim)

print(f"size: {matrix.size}", f"dim: {matrix.ndim}")

size: 4 dim: 1
size: 4 dim: 2

Numpy array vs list

Pole v knihovně numpy mají několik zásadních výhod pro numerické výpočty:

• Python seznamy (list) jsou příliž obecné, dynamicky typované a nepodporují matematické funkce.

• V numpy jsou pole staticky typované a homogenní - při vytvoření je určen typ, který je jednotný pro všechny prvky.

• Efektivní uložení v paměti, implementace matematických operací v rychlém jazyce (C, Fortran).

matrix.dtype

dtype('int32')

matrix_c = np.array([[1, 2], [3, 4]], dtype=complex)
matrix_c

array([[1.+0.j, 2.+0.j],
       [3.+0.j, 4.+0.j]])

Změnit typ lze vytvořením nové kopie pole nebo přes speciální funkce knihovny Numpy (np.int32(), np.float32(), …):

matrix[1,1] = 5.5
print(matrix[1,1])

matrix = np.array(matrix, dtype=float)
matrix[1,1] = 5.5
matrix[1,1]

5

5.5

matrix = np.float32(matrix)
matrix

array([[1. , 2. ],
       [3. , 5.5]], dtype=float32)

Pomocné generátory polí

V Numpy existuje množství pomocných funkcí, které výrazně zesnadňují vytváření polí:

arange() vygeneruje posloupnost, syntaxe je stejná jako range():

np.arange(0, 10, 1)  # argumenty: start, stop, step

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

np.arange(-1, 0, 0.1)

array([-1. , -0.9, -0.8, -0.7, -0.6, -0.5, -0.4, -0.3, -0.2, -0.1])

linspace() a logspace() vytváří posloupnosti s daným počtem prvků (budou se hodit obzvlášť při různých vizualizacích dat):

np.linspace(0, 10, 5)   # argumenty: start, stop, počet

array([ 0. ,  2.5,  5. ,  7.5, 10. ])

np.logspace(0, 10, 11, base=10)   # argumenty: start, stop, počet, základ logaritmu

array([1.e+00, 1.e+01, 1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06, 1.e+07,
       1.e+08, 1.e+09, 1.e+10])

ones() a zeros() vytvoří pole ze samých nul nebo jedniček:

np.ones(3)

array([1., 1., 1.])

Pokud chceme 2 a více rozměrů, musíme zadat rozměr jako tuple nebo list:

np.zeros([2, 3]), np.zeros((2, 3), dtype=int)

(array([[0., 0., 0.],
        [0., 0., 0.]]),
 array([[0, 0, 0],
        [0, 0, 0]]))

Indexování

Přístup k prvkům pole je analogický jako u Python seznamů. Pole jde stejným způsobem řezat.

matrix = np.array([[1, 2, 3, 4],
                   [5, 6, 7, 8],
                   [9, 10, 11, 12],
                   [13, 14, 15, 16]], dtype=int)
matrix

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12],
       [13, 14, 15, 16]])

matrix[1, 1]    # prvek na indexu (1,1)

6

Řez vybraným řádkem nebo sloupcem:

matrix[1, :]    # řez druhým řádkem

array([5, 6, 7, 8])

matrix[:, 1]    # řez druhým sloupcem

array([ 2,  6, 10, 14])

Řezy jsou mutable: pokud do nich něco přiřadíme, projeví se to na původním objektu:

matrix[:, 0] = 0
matrix

array([[ 0,  2,  3,  4],
       [ 0,  6,  7,  8],
       [ 0, 10, 11, 12],
       [ 0, 14, 15, 16]])

matrix[:, 0] = np.arange(4)
matrix

array([[ 0,  2,  3,  4],
       [ 1,  6,  7,  8],
       [ 2, 10, 11, 12],
       [ 3, 14, 15, 16]])

Úkol

Vyberte libovolnou submatici matice matrix o velikosti 2x2, transponujte a uložte ji do původní matice na stejné místo.

matrix[1:3,1:3] = matrix[1:3,1:3].transpose()
matrix

array([[ 1,  2,  3,  4],
       [ 5,  6, 10,  8],
       [ 9,  7, 11, 12],
       [13, 14, 15, 16]])

Vyřezávání pomocí pole indexů

V Numpy je navíc možné řezat pomocí pole indexů:

matrix[[1,3], :]    # výběr 2. a 4. řádku 

array([[ 1,  6,  7,  8],
       [ 3, 14, 15, 16]])

Výběr pomocí masky:

maska = [[True,False,False,True], 
        [False,False,False,False], 
        [False,False,False,False], 
        [True,False,False,True]]
print(type(maska))

matrix[maska]   # výběr rohových prvků

array([ 0,  4,  3, 16])

matrix[matrix % 3 == 0] # výběr prvků dělitelných 3

array([ 0,  3,  6, 12,  3, 15])

Append a Insert

Podobně jako u Python polí, Numpy poskytuje funkce na přidání prvku nakonec append() a na daný index insert():

array = np.arange(5)

array1 = np.append(array, -1)
array1

array([ 0,  1,  2,  3,  4, -1])

array2 = np.insert(array, 2, -1)
array2

array([ 0,  1, -1,  2,  3,  4])

1.4.2. Maticové operace

Součet/rozdíl matice a skaláru:

np.ones((3, 3)) + 1

array([[2., 2., 2.],
       [2., 2., 2.],
       [2., 2., 2.]])

Násobení/dělení skalárem:

np.arange(0, 5) * 2

array([0, 2, 4, 6, 8])

np.ones((3, 3)) / 4

array([[0.25, 0.25, 0.25],
       [0.25, 0.25, 0.25],
       [0.25, 0.25, 0.25]])

Násobení matic a vektorů se provádí pomocí funkce dot() nebo operátoru @:

# matice 2x3
A = np.array([[1,2,3],[4,5,6]])
print(A, A.shape, "\n")

# matice 3x2
B = np.array([[1,2],[3,4],[5,6]])
print(B, B.shape, "\n")

[[1 2 3]
 [4 5 6]] (2, 3) 

[[1 2]
 [3 4]
 [5 6]] (3, 2) 

C = np.dot(A,B) # součin matic
C, C.shape

(array([[22, 28],
        [49, 64]]),
 (2, 2))

C = A @ B # součin matic
C

array([[22, 28],
       [49, 64]])

Skalární součin dvou vektorů:

np.array([1, 2, 3]) @ np.array([3, 2, 1])

10

Pozor

Operace C*C násobí matice po prvcích (není to maticové násobení)!

# maticove nasobeni
print(np.dot(C,C), '\n')

# nasobeni po prvcich
print(C*C)

[[1856 2408]
 [4214 5468]] 

[[ 484  784]
 [2401 4096]]

Reshape

Funkce reshape() umožňuje změnit tvar pole/matice podle požadovaných rozměrů. Je třeba si ovšem dát pozor na indexové pořadí, podle kterého se prvky přerovnávají.

np.arange(1,17), np.reshape(np.arange(1,17), [4,4], order='F')  # pořadí indexů 'C' nebo 'F'

(array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16]),
 array([[ 1,  5,  9, 13],
        [ 2,  6, 10, 14],
        [ 3,  7, 11, 15],
        [ 4,  8, 12, 16]]))

1.4.3. Matematické funkce

numpy obsahuje často používané funkce a konstanty (napr. sqrt(), log(), log10(), sin(), abs(), e, pi, …):

print(np.sqrt(5))
print(np.log(5))
print(np.log10(5))
print(np.sin(5))
print(np.abs(-3))
print(np.e)
print(np.pi)

2.23606797749979
1.6094379124341003
0.6989700043360189
-0.9589242746631385
3
2.718281828459045
3.141592653589793

Součet prvků v poli je dán funkcí sum():

np.sum(np.arange(0, 100, 3))    # součet čísel dělitelných třemi od 0 do 100 

1683

Minimální a maximální hodnotu v poli určíme funkcí min() a max():

np.min(A), np.max(A)

(1, 6)

Polohu (index) minimální a maximální hodnoty v poli získáme pomocí funkce argmin() a argmax():

np.argmin(A), np.argmax(A)

(0, 5)

1.4.4. Další užitečné funkce

Náhoda

Pole náhodných čísel v rozmezí 0 az 1 se vygeneruje pomocí funkce np.random.rand():

np.random.rand(3,2)

array([[0.85196594, 0.66928364],
       [0.17104743, 0.51678847],
       [0.8152541 , 0.17603683]])

Statistické funkce

Funkce average() vrací průměrnou hodnotu; std() je směrodatná odchylka a var() je rozptyl:

np.average(A)   # průměrná hodnota

3.5

np.std(A)   # směrodaná odchylka (standard deviation)

1.707825127659933

np.var(A)   # rozptyl (variance)

2.9166666666666665

Práce se soubory - můžete se dozvědět zde

Tip

Více se můžete dozvědet v dokumentaci nebo opět v kurzu 12PYTH.

1.5. Vizualizace dat - matplotlib.pyplot

Pro vizualizaci dat v Pythonu existuje obsáhlá knihovna matplotlib.pyplot.

import numpy as np
import matplotlib.pyplot as plt

1.5.1. 1D plot

Možnost 1 - vykreslování ala Matlab

Vygenerujeme \(x\) a \(y\) hodnoty pro funkci sin():

x = np.linspace(0,4*np.pi,100)
y = np.sin(x)

Nejdříve je potřeba vytvořit obrázek pomocí figure(). Vykreslení dat pak provedeme příkazem plot(). Přidáme popisky os pomocí xlabel(), ylabel() a název grafu pomocí title():

plt.figure(0, figsize=(5,3))

plt.plot(x,y)   # vykreslení 1D grafu/funkce

plt.title('six(x)')
plt.xlabel('x')
plt.ylabel('y');

Knihovna matplotlib nabízí základní rozložení více grafů v jednom obrázku pomocí funkcí subplot() nebo subplots():

x = np.linspace(0,10,100)
y = np.exp(2*x)

plt.figure(0, figsize=(11,4))

plt.subplot(121)
plt.plot(x,y, label='exp(2x)')

plt.xlabel('x')
plt.ylabel('y')
plt.legend()

plt.subplot(122)
plt.plot(x,y, 'r--')

plt.xlabel('x')
plt.ylabel('y')
plt.legend(['y=$e^{2x}$'], fontsize=20, loc='upper left')  # LaTex výraz

plt.yscale('log')   # škála osy y
plt.ylim([0.1, 1e10]);

Možnost 2 - pokročilejší možnosti vykreslování

x = np.linspace(0,4*np.pi,100)
y = np.sin(x)

fig, axs = plt.subplots(2,2)    # 4 grafy v základním rozložení 2x2
fig.set_size_inches(10, 7)
fig.tight_layout()

axs[0,0].plot(x,y, '*')
axs[0,1].plot(x,y**2, 'g:')
axs[1,0].plot(x,y**3, 'k', linestyle='-.',)
axs[1,1].plot(x,y**4, color='red', linestyle='dashed', linewidth=2, label='sin(x)', alpha=0.5)

axs[0,0].set_xlabel('x')
axs[0,0].set_ylabel('sin(x)')
axs[0,0].set_title('Graf funkce sin(x)')
axs[0,0].legend(['sin(x)'])

axs[1,1].legend();

Uložení obrázku

Na závěr obrázek uložíme příkazem savefig():

fig.savefig("obrazek.png", dpi=300)

1.5.2. 2D plot

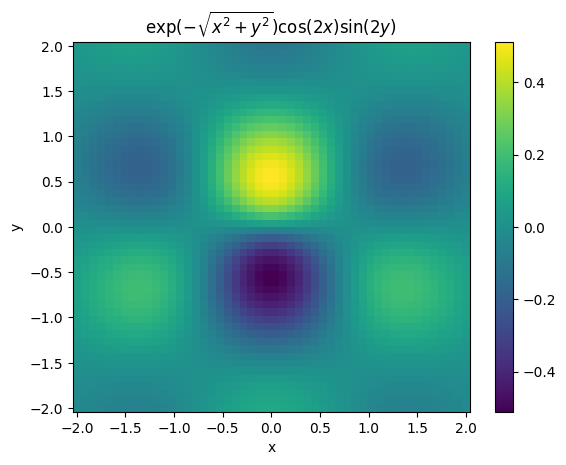
Mějme funkci \(z(x,y)\), která závisí na dvou proměnných: \( \begin{equation} z(x,y)=\exp(-\sqrt{x^2+y^2})\cos(2x)\sin(2y), \end{equation} \) a vykreslíme její závislost v 2D grafu.

Vytvoříme mřížku \(x\times y\) pomocí funkce meshgrid():

osa_x = np.linspace(-2, 2, 50)
osa_y = np.linspace(-2, 2, 50)
(x,y) = np.meshgrid(osa_x, osa_y);

Spočítáme hodnoty funkce \(z(x,y)\):

z = np.exp(-np.sqrt(x**2 + y**2)) * np.cos(2*x) * np.sin(2*y)

plt.pcolormesh(x,y,z,shading='auto')
plt.xlabel('x')
plt.ylabel('y')
plt.title('$\exp(-\sqrt{x^2+y^2})\cos(2x)\sin(2y)$')
plt.colorbar();

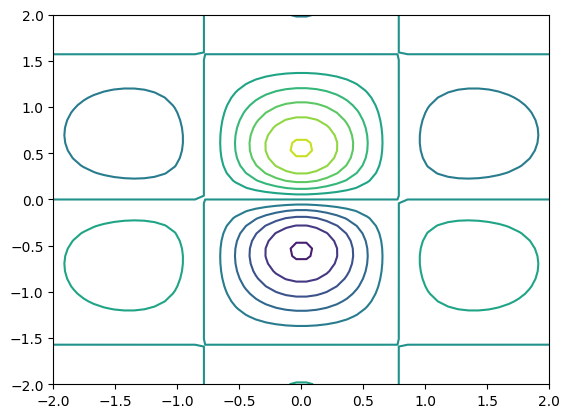
Kontury získáme použitím funkce contour():

plt.contour(x,y,z, levels=10);

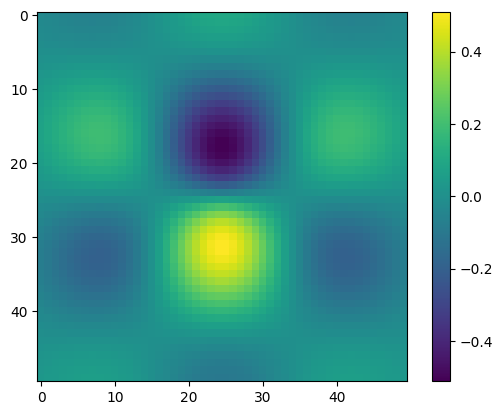
Plot obrázku pomocí funkce imshow():

plt.imshow(z)
plt.colorbar();

1.5.3. Další typy grafů

Knihovna obsahuje řadu dalších nástrojů a typů grafů, které je možné vykreslit. Obsáhlejší, přesto stále stručný, popis knihovny najdete opět zde.

Seznam všech dostupných typů grafů najdete v dokumentaci knihovny.

Tady jen zmíníme některé z často používaných typů grafů:

• scatter() - bodový graf

• bar() - schodový graf

• hist(), hist2d() - histogram 1D a 2D dat

• contour() - kontury 2D funkce

• streamplot() - vektorové pole

• plot_surface() - 3D plot, vykreslení funkce dvou proměnných

1.6. Knihovna Scipy

SciPy je základní referenční knihovnou, obsahující nástroje pro vědecké výpočty. Najdeme v ní např. speciální funkce, interpolace, Fourierovu transformaci, numerické integrátory a mnohé další. Naším cílem bude ukázat některé z funkcí SciPy.

Knihovna scipy obsahuje ředu užitečných modulů:

import scipy.linalg         # lineární algebra
import scipy.constants      # důležité fyzikální a další konstanty
import scipy.interpolate    # interpolace funkcí
import scipy.optimize       # optimalizace, hledaní extrémů
import scipy.integrate      # numerická integrace a řešení ODR

c:\Users\jiral\AppData\Local\Programs\Python\Python310\lib\site-packages\scipy\__init__.py:146: UserWarning: A NumPy version >=1.16.5 and <1.23.0 is required for this version of SciPy (detected version 1.26.2
  warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"

Poznámka

V Numpy také existuje modul np.linalg, ale oproti modulu knihovny scipy není zdaleka tak rozsáhlý.

Příklad využití modulu konstant:

from scipy.constants import pi, golden_ratio, c
print(pi, golden_ratio, c)

Dále si ukážeme příklady využití funkcí z různých modulů na úlohách, se kterými jste se setkali v první části tohoto kurzu.

1.6.1. Řešení soustav rovnic, vlastní čísla matice

import numpy as np
import scipy.linalg as la

Soustava lineárních rovnic

Řešíme soustavu lineárních rovnic: \( \mathbb{A} \vec{x} = \vec{b} \)

A = np.array([[8,2,3],[2,5,6],[7,8,2]])
b = np.array([10,11,12])

x  = la.solve(A, b)  # řešení soustavy Ax = b
x

array([0.6877193 , 0.62807018, 1.08070175])

Řešení přes inverzi matice \(\mathbb{A}^{-1}\):

Ainv = la.inv(A)  # inverze matice A
x = Ainv @ b
x

array([0.6877193 , 0.62807018, 1.08070175])

Vlastní čísla matice

A = np.array([[0,2,0],[2,0,1],[2,1,0]])

eig_nums, eig_vects = la.eig(A)
print("Vlastní čísla:\n" + str(eig_nums))
print("Vlastní vektory:\n" + str(eig_vects))

Vlastní čísla:
[-1.56155281+0.j  2.56155281+0.j -1.        +0.j]
Vlastní vektory:
[[-0.67127345  0.48332441 -0.53452248]
 [ 0.52411447  0.6190305   0.26726124]
 [ 0.52411447  0.6190305   0.80178373]]

Ověření:

A @ eig_vects[:, 0], eig_nums[0] * eig_vects[:, 0]  # A*v1 = e1*v1

(array([ 1.04822894, -0.81843243, -0.81843243]),
 array([ 1.04822894-0.j, -0.81843243+0.j, -0.81843243+0.j]))

LU dekompozice

P, L, U = la.lu(A)
P, L, U

(array([[0., 1., 0.],
        [1., 0., 0.],
        [0., 0., 1.]]),
 array([[1. , 0. , 0. ],
        [0. , 1. , 0. ],
        [1. , 0.5, 1. ]]),
 array([[ 2.,  0.,  1.],
        [ 0.,  2.,  0.],
        [ 0.,  0., -1.]]))

Ověření:

P @ (L @ U), A

(array([[0., 2., 0.],
        [2., 0., 1.],
        [2., 1., 0.]]),
 array([[0, 2, 0],
        [2, 0, 1],
        [2, 1, 0]]))

1.6.2. Aproximace funkcí, interpolace

import numpy as np
from scipy import linalg, interpolate, special
import matplotlib.pyplot as plt

c:\Users\jiral\AppData\Local\Programs\Python\Python310\lib\site-packages\scipy\__init__.py:146: UserWarning: A NumPy version >=1.16.5 and <1.23.0 is required for this version of SciPy (detected version 1.26.2
  warnings.warn(f"A NumPy version >={np_minversion} and <{np_maxversion}"

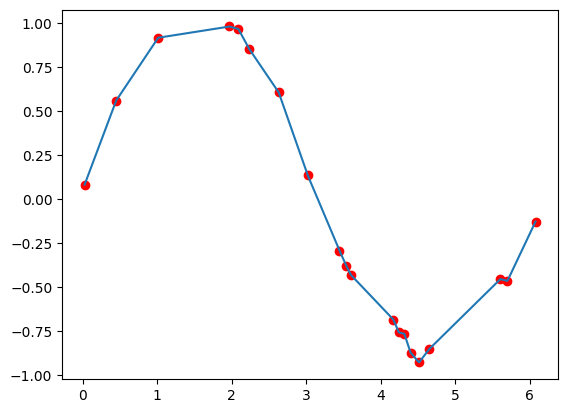
Lineární interpolace

np.random.seed(194)

x_p = np.random.rand(20) * 2*np.pi
y_p = np.random.rand(20)/5 + np.sin(x_p)


x = np.linspace(np.min(x_p), np.max(x_p), 1000)

y = interpolate.interp1d(x_p, y_p)(x)

plt.plot(x_p, y_p, 'ro')
plt.plot(x, y, '-')

[<matplotlib.lines.Line2D at 0x23d6988aa10>]

Interpolace Lagrangeovým polynomem

yL = interpolate.lagrange(x_p, y_p)

plt.plot(x_p, y_p, 'ro')
plt.plot(x, yL(x), '-')

[<matplotlib.lines.Line2D at 0x23d69915c90>]

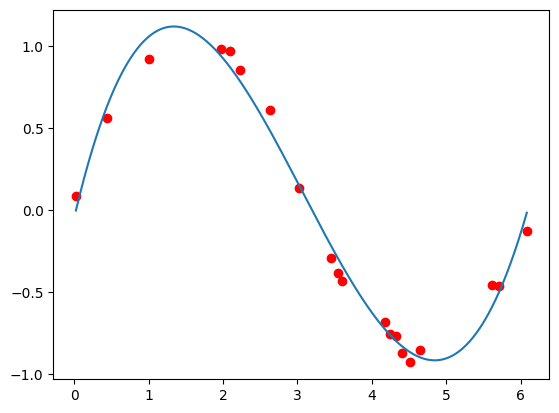
Least-squares fit

Proložení bodů polynomem pomocí metody nejmenších čtverců (np.polyfit()).

coeffs = np.polyfit(x_p, y_p, 4)

yP= np.poly1d(coeffs)

plt.plot(x_p, y_p, 'ro')
plt.plot(x, yP(x), '-')

[<matplotlib.lines.Line2D at 0x23d6aa25780>]

1.6.3. Třídění

import numpy as np

arr = [1, 8, 4, 3, -5, 7, 11, 2, 1]
np.sort(arr, kind='quicksort')  # kind='quicksort', 'mergesort', 'heapsort', 'stable'

array([-5,  1,  1,  2,  3,  4,  7,  8, 11])

Další funkce si představíme v následujících cvičeních.

Více se opět můžete dozvědět v oficiální dokumentaci knihovny.

1.7. Bonus

Úkol - bonus 1

Doplňte chybějící části označené ??? a opravte chyby, aby fungoval program na hru Oko bere (Black jack):

import random

soucet = 0
while (soucet < 21):
    print('Máš', soucet, 'bodů')
    odpoved = input('Otočit kartu? ')
    if odpoved == 'ano':
        karta = random.randrange(2, 11)
        print('Otočil/a jsi', karta)
        soucet += karta
    elif odpoved == 'ne':
        break
    else:
        print("Zadal jsi špatný příkaz!")

if soucet == 21:
    print('Gratuluji! Vyhrál/a jsi!')
elif soucet > 21: 
    print('Smůla!', soucet, 'bodů je moc!')
else:
    print('Chybělo jen', 21 - soucet, 'bodů!')    

Máš 0 bodů
Zadal jsi špatný příkaz!
Máš 0 bodů
Otočil/a jsi 5
Máš 5 bodů
Otočil/a jsi 10
Máš 15 bodů
Otočil/a jsi 3
Máš 18 bodů
Otočil/a jsi 6
Smůla! 24 bodů je moc!

Úkol - bonus 2

1. Implementujte třídící metodu Selection sort.

2. Implementujte Quicksort.

Pro nápovědu se můžete podívat do materiálu jiných cvičení zde.

Tip

V Pythonu lze prohodit hodnotu dvou proměnných pomocí výrazu a,b = b,a (v C++ funkce swap(a,b)).

import numpy as np

1. Selection sort

arr = [1, 8, 4, 3, -5, 7, 11, 2, 1]

ind = 0  #  počet setřízených prvků

while (ind < len(arr) - 1):
    i = np.argmin(arr[ind:])  # najdu index nejmenšího prvku v podsekvenci od indexu 'ind' dále
    arr[ind], arr[ind + i] = arr[ind + i], arr[ind]  # hodím nejmenší číslo na konec již setřízené posloupnosti
    ind += 1

arr  

[-5, 1, 1, 2, 3, 4, 7, 8, 11]

2. Quicksort

Implementace pomocí rekurze. Funkce quicksort() rozdělí prvky podle hodnoty prvního prvku (pivota) na menší a větší. Pak rekurzivně zavolá sama sebe na obě tyto skupiny prvků.

arr = np.array([1, 8, 4, 3, -5, 7, 11, 2, 1])

def quicksort(arr):
    if (len(arr) <= 1):
        return arr
    
    pivot = arr[0]
    
    smallerIdx = arr < pivot  # maska
    biggerIdx = arr > pivot   # maska
    
    smaller = []
    bigger = []
    
    smaller = quicksort(arr[smallerIdx])
    bigger = quicksort(arr[biggerIdx])
    
    return np.concatenate((smaller, [pivot], bigger))

quicksort(arr)    

array([-5,  1,  2,  3,  4,  7,  8, 11])