6. Řešení diferenciálních rovnic s okrajovou podmínkou

V předchozím cvičení jsme se zabývali metodami na řešení počáteční úlohy tvaru:

\[ \frac{d \vec{y}}{dx} = f(x, \vec{y}), \quad \vec{y}(0) = \vec{y}_0. \]

Tato úloha představuje soustavu obyčejných diferenciálních rovnic 1. řádu s počáteční podmínkou \(\vec{y}(0) = \vec{y}_0\). Tedy známe řešení \(\vec{y}\) v nějakém konkrétním bodě.

V dnešním cvičení si představíme numerické metody řešící okrajové úlohy. Oproti počáteční úloze budeme znát část řešení ve více bodech. Pro \(N=2\) můžeme například mít \(y_0(0) = 0\) a \(y_1(1) = 0\) nebo \(y_0(0) = 0\) a \(y_0(1) = 0\). Druhý případ je běžnější, proto se dále budeme zabývat pouze jím.

Omezíme se na řešení soustavy dvou ODR, která odpovídá diferenciální rovnici druhého řádu:

\[ y^{\prime \prime} = f(x, y(x), y^{\prime}(x)), \quad x \in [a, b], \quad y(a) = \alpha_1, \quad y(b) = \alpha_2, \]

kde máme dvě okrajové podmínky pro funkci \(y\) v bodech \(a\) a \(b\). Okrajová úloha již nelze řešit stejným způsobem, jako počáteční. Neznáme totiž celé jednoznačné řešení (hodnotu funkce \(y\) i její derivace \(y^{\prime}\)) v jednom konkrétním bodě, ze kterého bychom mohli řešení vyvíjet - integrovat pravou stranu soustavy ODR.

Zde si představíme dvě metody na řešení okrajových úloh:

• Metoda střelby

• Metoda sítí (konečných diferencí)

Potřebné knihovny:

import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg, integrate, optimize

Pomocí metod budeme řešit následující úlohu, která odpovídá rovnici tlumeného oscilátoru:

\[ y^{\prime \prime} \left( t \right) + 2 \zeta \omega_0 y^{\prime} \left( t \right) + \omega_0^2 y \left( t \right) = 0, \quad t \in [0, \, 2], \quad y \left( 0 \right) = 1, \quad y \left( 2 \right) = 0, \]

kde \(\omega_0 = 10\) je vlastní frekvence oscilátoru a \(\zeta = \frac{1}{10}\) je tlumící faktor.

Rovnice má obecné řešení:

\[ y(t) = A e^{-\zeta \omega_0 t} \sin{\left(\sqrt{1 - \zeta^2} \omega_0 t + \varphi\right)} \]

Pro naší volbu koeficientů a okrajové podmínky máme:

\[ y \left( t \right) = -\frac{\exp{\left( -t \right)} \sin \left[ 3 \sqrt{11} \left( t - 2 \right) \right]}{\sin \left( 6 \sqrt{11} \right) } \]

na intervalu \( t \in [0, 2] \).

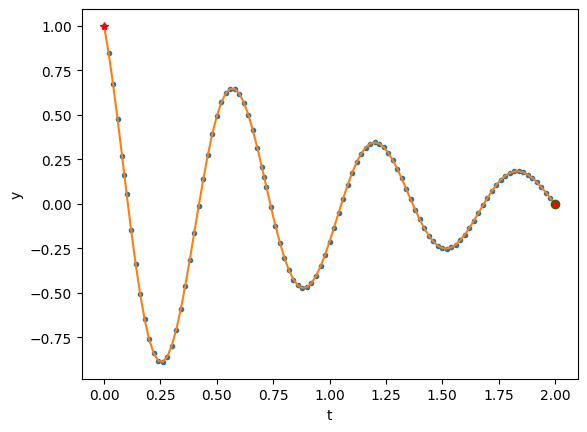
# analyticke reseni rovnice tlumeneho oscilatoru

def y_sol(t):
    return -(np.exp(-t) * np.sin(3 * np.sqrt(11) * (t - 2))) / np.sin(6*np.sqrt(11))

tt = np.linspace(0, 2, 100)
plt.plot([0, 2], [1, 0], 'r*')
plt.plot(tt, y_sol(tt));

6.1. Metoda střelby

Tato metoda je inspirovaná úlohou střelby na cíl v homogenním gravitačním poli Země.

Řekněme, že máme kanón na pozici \(x = a\) a cíl na pozici \(x = b\). Zřejmě nás zajímá, pod jakým úhlem vystřelit a jakou silou (kolik použít střelného prachu), aby koule zasáhla cíl. Víme, že hmotný objekt se v gravitačním poli Země řídí pohybovou rovnicí (zde neuvažujeme odpor vzduchu):

\[ m \ddot{\vec{r}} = - m\vec{g}. \]

Na začátku známe pouze polohu kanónu a cíle, což odpovídá:

\[ \vec{r}(0) = [x_0, y_0] = [a, 0], \quad \vec{r}(T) = [x_T, y_T] = [b, 0], \]

kde \(T\) značí čas dopadu koule zpátky na zem. Tato úloha je okrajovou úlohou, jelikož známe použe část řešení (polohy ale ne rychlosti) na začátku a na konci. Bez znalosti počátečních rychlostí (velikosti rychlosti a náměru děla) nedokážeme řešení vyvíjet integrováním pravé strany. Metodu střelby si dále ukázeme na obecné diferenciální rovnici 2. řádu a k úloze střelby z kanónu se vrátíme v zápočtovém úkolu 5.

Uvažujme opět následující okrajovou úlohu s ODR druhého řádu:

\[ y^{\prime \prime} = f(x, y(x), y^{\prime}(x)), \quad x \in [a, b], \quad y(a) = \alpha_1, \quad y(b) = \alpha_2, \]

Řešení pomocí metody střelby spočívá v následujících krocích:

1. náhodně zvolíme počáteční hodnotu derivace \(y^{\prime}(a) = \beta\)

2. vyřešíme počáteční úlohu:

\[\begin{split} \begin{align} & y^{\prime}(x) = z(x), \quad &y(a) = \alpha_1 \\ & z^{\prime}(x) = f(x, y(x), z(x)), \quad &z(a) = y^{\prime}(a) = \beta \end{align} \end{split}\]

3. tím získáme \(y(b; \beta)\)

4. řešíme nelineální rovnici \(F(\beta) = y(b; \beta) - \alpha_2 = 0\) tím, že opakujeme kroky 1-3

Na krok 4 je možné aplikovat libovolnou z metod představených v předchozím cvičení. Jednoduchou volbou je bisekce, tedy máme na začátku dva odhady \(\beta_1\) a \(\beta_2\) takové, že \(F(\beta_1) F(\beta_2) < 0\) (jednou přestřelíme cíl, podruhé podstřelíme). V následujícím kódu použijeme Newton-Raphsonovu metodu.

Ukážeme si implementaci metody střelby na úloze tlumeného oscilátoru. Počáteční úloha z bodu 2 metody vypadá následovně:

\[\begin{split} \begin{align} & y^{\prime}(t) = z(t), \quad &y(0) = 1 \\ & z^{\prime}(t) = -2 z(t) - 100 y (t), \quad &z(0) = y^{\prime}(0) = \beta \end{align} \end{split}\]

# definice prave strany pocatecni ulohy
def f(t, Y):
    y, z = Y  # Y je vektor reseni [y, z]
    return np.array([z, -2*z - 100*y])

# okrajove podminky
x0 = 0
x1 = 2
y0 = 1
y1 = 0

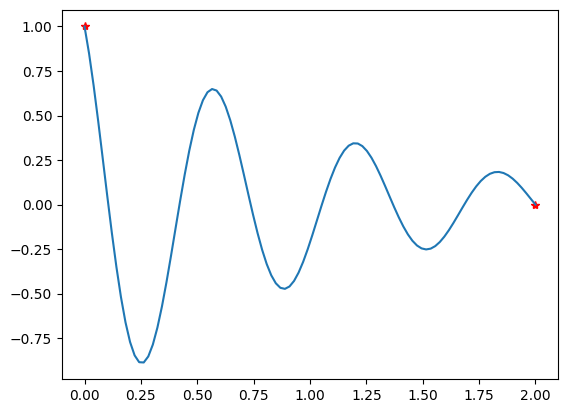
Řešení počáteční úlohy pro jednu konkrétní volbu \(\beta\):

beta = -100

# druha pocatecni podminka
z0 = beta

res = integrate.solve_ivp(f, [x0, x1], [y0, z0], method='RK45', t_eval = tt)

plt.plot(res.t, res.y[0])  # y[0] odpovida y, y[1] odpovida z=y'
plt.plot([2], [res.y[0, -1]], 'go')
plt.plot([0, 2], [y0, y1], 'r*')
plt.xlabel('t')
plt.ylabel('y');

Implementace metody střelby

Úkol

Pomocí metody střelby řešte úlohu tlumeného oscilátoru.

Defininujte funkci \(F(\beta)\) podle postupu metody střelby. Najděte kořen této funkce (beta_root) pomocí knihovní funkce optimize.root_scalar(..., method='newton'). Budete potřebovat také darivaci funkce \(F(\beta)\). Použijte aproximaci této derivace pomocí dopředné diference (numerická derivace).

def F(beta):
    ## DOPLŇTE - definice funkce na hledani korene ##
    return None

# numericka derivace
def dF(beta, h = 0.00001): 
    ## DOPLŇTE - numericka derivace funkce F(beta) ##
    return None

## DOPLŇTE - hledani korene, Newton-Ralphson ##
res_root = optimize.root_scalar(F, fprime=dF, x0=0, method='newton', rtol=1e-6)

print(res_root)
beta_root = res_root.root

      converged: True
           flag: 'converged'
 function_calls: 8
     iterations: 4
           root: array([-6.65510418])

Vizualizace řešení

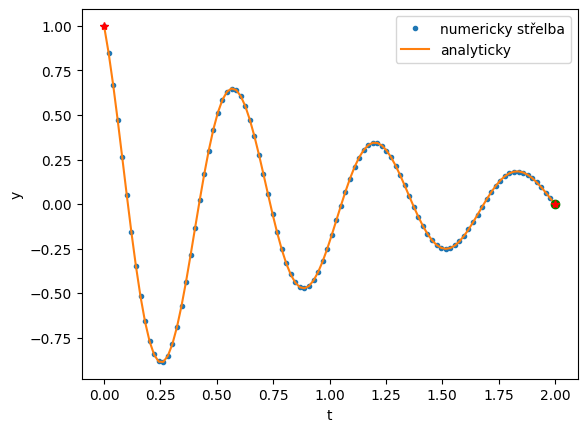
Nalezením kořene \(\beta^{*}\), \(F(\beta^{*}) = 0\), jsme získali počáteční podmínku takovou, že okrajová a počáteční úloha jsou ekvivalentní. Okrajovou úlohu vyřešíme vyřešením počáteční úlohy s \(z(0) = \beta^{*}\):

res_ivp = integrate.solve_ivp(f, [x0, x1], [y0, beta_root], method='RK45', t_eval = tt)

plt.plot(res_ivp.t, res_ivp.y[0], '.', label='numericky střelba')  # y[0] odpovida y, y[1] odpovida z=y'
plt.plot(res_ivp.t, y_sol(res_ivp.t), '-', label='analyticky')  # presne reseni
plt.plot([2], [res_ivp.y[0, -1]], 'go')
plt.plot([0, 2], [y0, y1], 'r*')
plt.xlabel('t')
plt.ylabel('y')
plt.legend();

# srovnani reseni na pravem okraji
res_ivp.y[0][-1], y_sol(x1)

(-2.7755575615628914e-17, -0.0)

6.2. Metody sítí (konečných diferencí)

Metoda konečných diferencí, také nazývaná metodou sítí nebo relaxační metodou, je založená na nahrazení derivací v diferenciální rovnici pomocí konečných diferencí. Tím získáme algebraický výraz, který již dokážeme řešit na počítači. Uvažujeme následující ODR 2. řádu s okrajovou podmínkou:

\[ p \left(x \right) y^{\prime \prime} \left( x \right) + q \left(x \right) y^{\prime} \left( x \right) + r \left(x \right) y \left( x \right) + s \left(x \right) = 0, \quad x \in [a, b], \quad y(a) = \alpha_1, \quad y(b) = \alpha_2. \]

Provedeme nahrazení jednotlivých derivací pomocí následujících aproximací pomocí konečných diferencí, které počítáme na rovnoměrné síti na intervalu \([a, b]\) s krokem \(h\):

\[ y_i^{\prime} \approx \frac{y_{i + 1} - y_{i}}{h} \quad \mathrm{a} \quad y_i^{\prime \prime} \approx \frac{y_{i + 1} - 2 y_{i} + y_{i - 1}}{h^2}, \quad i = 0, \dots, n - 1. \]

Okrajovou úlohu pak můžeme přepsat jako soustavu lineárních algebraických rovnic:

\[ \tilde{p_i} y_{i - 1} + \tilde{q_i} y_i + \tilde{r_i} y_{i + 1} = \tilde{s_i}, \quad y_0 = \alpha_1, \quad y_{n - 1} = \alpha_2, \]

kde \( \tilde{p_i} = p_i \), \( \tilde{q_i} = \left( -2 p_i - q_i h + r_i h^2 \right) \), \( \tilde{r_i} = \left(p_i + q_i h \right) \) a \( \tilde{s_i} = -s_i h^2 \).

V maticové formě má systém lineárních rovnic tvar:

\[\begin{split} \begin{pmatrix} 1 & & & & \\ \tilde{p}_1 & \tilde{q}_1 & \tilde{r}_1 & & \\ & \ddots & \ddots & \ddots & \\ & & \tilde{p}_{n - 2} & \tilde{q}_{n - 2} & \tilde{r}_{n - 2} \\ & & & & 1 \\ \end{pmatrix} \begin{pmatrix} y_0 \\ y_1 \\ \vdots\\ y_{n-2} \\ y_{n-1} \end{pmatrix} = \begin{pmatrix} \alpha_1 \\ \tilde{s}_1 \\ \vdots \\ \tilde{s}_{n-2} \\ \alpha_2 \end{pmatrix}. \end{split}\]

Tato metoda se někdy nazývá relaxační metodou, jelikož typicky řešíme velkou soustavu linearních rovnic pomocí iteračního algoritmu. Tedy máme nějaký počáteční odhad, který iteračně zlepšujeme (viz předchozí kapitola). V případě diferenciální rovnice 2. řádu vidíme, že soustava je třidiagonální, stačilo by tedy využít Thomasova algoritmu!

Pomocí této metody budeme opět řešit úlohu tlumeného oscilátoru:

\[ y^{\prime \prime} \left( t \right) + 2 y^{\prime} \left( t \right) + 100 y \left( t \right) = 0, \quad t \in [0, \, 2], \quad y \left( 0 \right) = 1, \quad y \left( 2 \right) = 0. \]

Postup metody konečných diferencí lze shrnout do následujících kroků:

1. Zvolíme tvar konečných diferencí, kterými nahradíme jednotlivé derivace.

2. Získáme soustavu lineárních rovnic - sestavíme matici soustavy a pravou stranu.

3. Řešíme soustavu pomocí zvoleného algoritmu.

Implementace metodu konečných diferencí

Úkol

Pomocí metody konečných diferencí řešte úlohu tlumeného oscilátoru.

a = 0
b = 2

# okrajove podminky
alpha1 = 1
alpha2 = 0

## 1. volíme diference podle predchoziho popisu pro obecnou ODR 2. radu
N = 101  # velikost site
h = (b - a) / (N-1)
tt = np.linspace(a, b, N)

## 2. sestaveni matice a prave strany

# koeficienty p_i, q_i, r_i a s_i nezavisi na t !
p_i = 1
q_i = -2 - 2*h + 100*h**2
r_i = 1 + 2*h
s_i = 0

# matice soustavy
A = np.zeros([N, N])
A[0,0] = A[-1,-1] = 1
idx = np.arange(0, N-1)
A[idx[:-1]+1,idx[:-1]] = p_i        # spodni vedlejsi diagonala
A[idx[1:],idx[1:]] = q_i  # diagonala
A[idx[1:],idx[1:]+1] = r_i  # diagonala

# prava strana
b = np.zeros(N)
b[0] = alpha1
b[1:-1] = s_i
b[-1] = alpha2

## 3. vyreseni soustavy
y = linalg.solve(A, b)

A, b

(array([[ 1.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
        [ 1.  , -2.  ,  1.04, ...,  0.  ,  0.  ,  0.  ],
        [ 0.  ,  1.  , -2.  , ...,  0.  ,  0.  ,  0.  ],
        ...,
        [ 0.  ,  0.  ,  0.  , ..., -2.  ,  1.04,  0.  ],
        [ 0.  ,  0.  ,  0.  , ...,  1.  , -2.  ,  1.04],
        [ 0.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  1.  ]]),
 array([1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
        0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]))

Vizualizace řešení

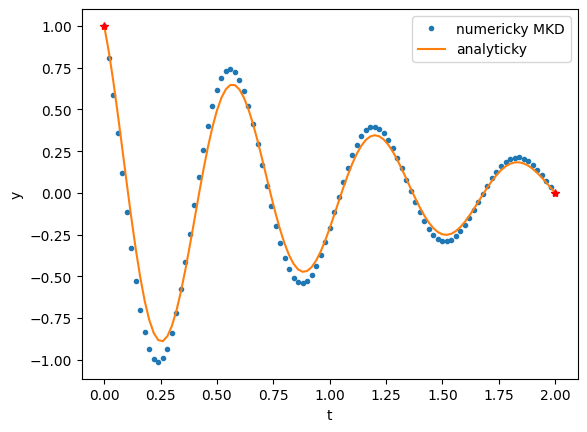
plt.plot(tt, y, '.', label='numericky MKD')  # y[0] odpovida y, y[1] odpovida z=y'
plt.plot(tt, y_sol(tt), '-', label='analyticky')  # presne reseni
plt.plot([0, 2], [y0, y1], 'r*')
plt.xlabel('t')
plt.ylabel('y')
plt.legend();

Knihovna SciPy poskytuje funkci scipy.integrate.solve_bvp() pro řešení okrajových úloh:

y_init = np.zeros([2,N])  # pocatecni odhad
res_bvp = integrate.solve_bvp(f, lambda ya, yb: np.array([ya[0]-alpha1, yb[0] - alpha2]), tt, y_init)
#print(res_bvp)

plt.plot(res_bvp.x, res_bvp.y[0], '.', label='numericky střelba')  # y[0] odpovida y, y[1] odpovida z=y'
plt.plot(res_bvp.x, y_sol(res_bvp.x), '-', label='analyticky')  # presne reseni
plt.plot([2], [res_bvp.y[0, -1]], 'go')
plt.plot([0, 2], [y0, y1], 'r*')
plt.xlabel('t')
plt.ylabel('y');