Řešení nelineárních rovnic#
V této kapitole si představíme několik algoritmů a metod na řešení jedné nebo soustavy nelineárních rovnic.
Oproti linearním rovnicím budeme vždy potřebovat počátečný odhad řešení, který budeme iteračně zpřesňovat určitou metodou.
U metod nás bude zajímat:
rychlost konvergence - počet kroků potřebných k dosažený požadovené přesnosti
jistota konvergence - jestli máme zajištěno, že metoda skončí v bodě, kde se nachází řešení a ne např. v lokálním extrému
Řešení jedné rovnice#
Pokud řešíme pouze jednu rovnici, lze snadno využít určité prioritní znalosti jak funkce vypadá, a omezit hledání řešení (kořenů) pouze na určitý interval. Existuje řada jednoduchých metod, které umožňují nalézt řešení v zadaném intervalu. Řešíme úlohu:
řešíme \(f(x)=0\)
předpokládáme pěkné, spojité funkce
obecný postup:
ohraničení kořenů - určení intervalů, které obsahují alespoň jeden kořen
pokud pro \(a<b\) platí, že \(f(a)f(b)<0\), pak je v intervalu \((a,b)\) alespoň jeden kořen
zpřesňování hodnoty kořene
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve, root_scalar
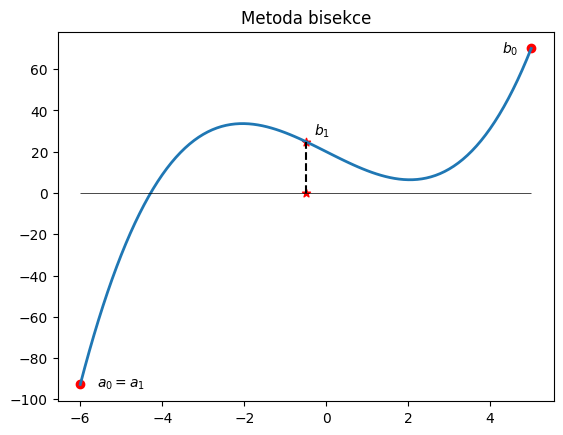
Metoda půlení intervalu (bisekce)#
postup
nechť je kořen leží v intervalu \((a_{0},b_{0})\), tedy platí \(f(a_{0})f(b_{0})<0\)
vypočítáme \(c_0 = (a_{0}+b_{0})/2\)
jeden krajní bod ponecháme, druhý posuneme do \(c_0\), aby opět platilo \(f(a_{1})f(b_{1})<0\)
\(a_1 = a_0\) a \(b_1 = c_0\) nebo \(a_1 = c_0\) a \(b_1 = b_0\)
skončíme v momentě, kdy je relativní chyba menší než požadovaná
po \(n\)-tém kroku je kořen omezený body \(a_{n}\) a \(b_{n}\)
nepřesnost určení kořene: \(r_n(x)= \frac{\lvert b_{n}-a_{n}\rvert}{|c_n|}\), kde \(c_n\) je odhad řešení v kroce \(n\) a platí: \(r_{n+1}=r_{n}/2\)
vždy konverguje (pokud interval obsahuje kořen)
v blízkosti kořene pomalá
Analýza funkce
Uvažujeme funkci: \(f(x) = 0.8 x^3 - 10 x + 20\)
def f(x):
return 0.8 * x**3 - 10*x + 20
# pocatecni body omezujici reseni
a0 = -6
b0 = 5
# vykresleni funkce
x = np.linspace(-6, 5, 100)
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=-6, xmax=5)
plt.scatter([a0, b0], [f(a0), f(b0)], c='r')
# vizualizace kroku
plt.plot([(a0+b0)/2, (a0+b0)/2], [0, f((a0+b0)/2)], 'k--')
plt.scatter([(a0+b0)/2, (a0+b0)/2], [0, f((a0+b0)/2)], c='r', marker='*')
plt.text(4.3,68,'$b_0$')
plt.text(-5.6,-94,'$a_0=a_1$')
plt.text(-0.3,28,'$b_1$')
plt.title('Metoda bisekce');
Algoritmus bisekce
Implementujte metodu bisekce doplněním následujícího kódu.
Do pole reseni uložte vždy řešení a do pole epsilon odpovídající chybu v každé iteraci.
eps = 1e-15 # pozadovana chyba
iteraci_max = 100 # max. iteraci
a = a0
b = b0
# budeme si prubezne ukladat odhad reseni a chybu odhadu
epsilon = np.ones(iteraci_max) # odhad relativni chyby, tedy delku intervalu <a,b> v jednotlivych krocich
reseni = np.zeros(iteraci_max) # aktualni odhad reseni
i = 0
## DOPLŇTE ##
iteraci_end = i
koren = reseni[i-1] # odhad konecneho reseni
chyba = epsilon[i-1] # odhad konecne chyby
print(koren, iteraci_end, chyba)
-4.2822890178707524 51 5.185184932600293e-16
Porovnání s výsledkem funkce root_scalar() z knihovny SciPy, která umí metodu bisekce:
koren_SP = root_scalar(f, bracket=[a0, b0], method="bisect", rtol=1e-15).root
print(koren, f(koren), chyba)
print(koren_SP, f(koren_SP)) # srovnání s funkcí z knihovny SciPy
-4.2822890178707524 -2.1316282072803006e-14 5.185184932600293e-16
-4.282289017871449 -2.3703705664956942e-11
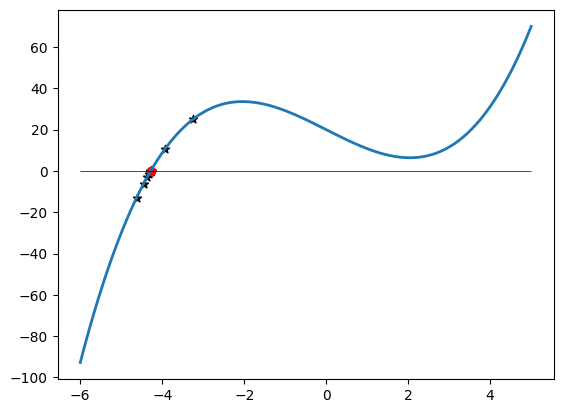
Vizualizace nalezeného kořenu
# vykresleni reseni
x = np.linspace(-6, 5, 100)
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=-6, xmax=5)
plt.scatter(reseni[:iteraci_end], f(reseni[:iteraci_end]), c='k', marker='*')
plt.scatter(koren, f(koren), c='r');
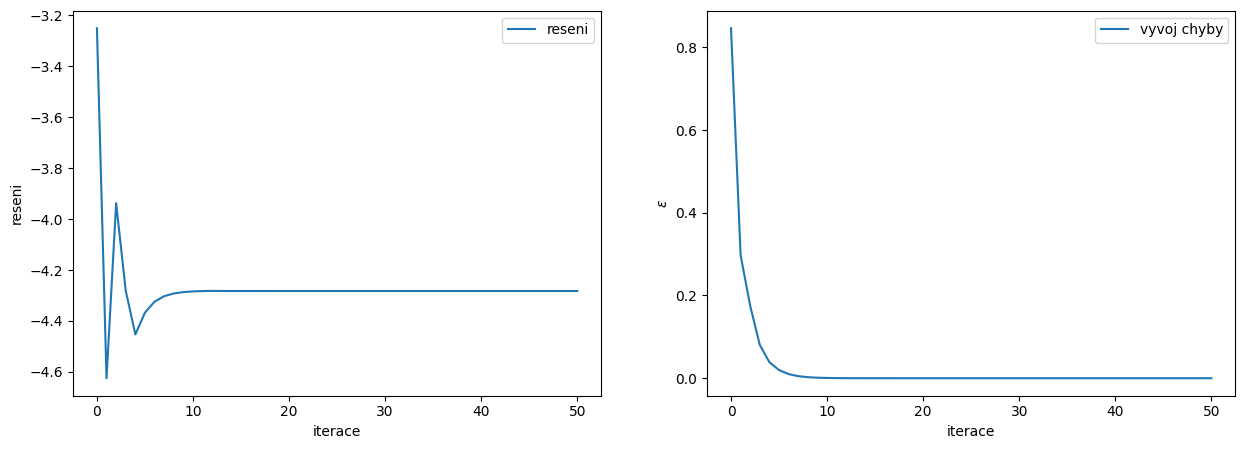
Analýza konvergence
fig, ax = plt.subplots(1,2,figsize=(15,5))
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci_end),reseni[:iteraci_end],label='reseni')
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci_end),epsilon[:iteraci_end],label='vyvoj chyby')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
#ax[1].set_yscale('log')
ax[1].legend();
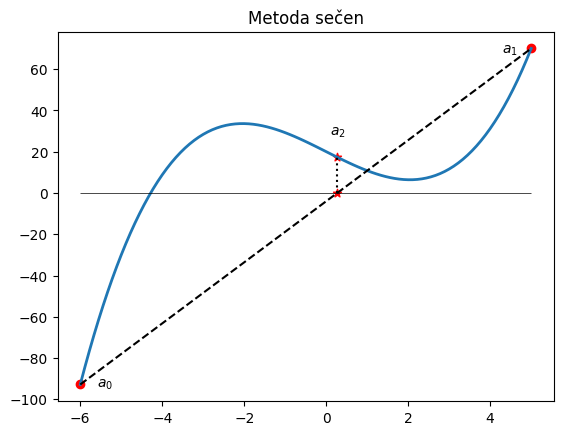
Metoda sečen#
postup
mějme body \(a_{n-1}\) a \(a_{n}\)
zvolíme \(a_{n+1}\) v průsečíku spojnice bodů \(\left(a_{n-1},y(a_{n-1})\right)\) a \(\left(a_{n},y(a_{n})\right)\) s osou \(x\):
\[ a_{n+1} = \frac{a_{n-1} f(a_{n}) - a_{n} f(a_{n-1})}{f(a_{n}) - f(a_{n-1})} \]konvergence není zaručena
# vykresleni funkce
x = np.linspace(-6, 5, 100)
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=-6, xmax=5)
plt.scatter([a0, b0], [f(a0), f(b0)], c='r')
# vizualizace kroku
c = (a0*f(b0)-f(a0)*b0) / (f(b0)-f(a0))
plt.plot([a0, b0], [f(a0), f(b0)], 'k--')
plt.plot([c, c], [0, f(c)], 'k:')
plt.scatter([c, c], [0, f(c)], c='r', marker='*')
plt.text(4.3,68,'$a_1$')
plt.text(-5.6,-94,'$a_0$')
plt.text(0.1,28,'$a_2$')
plt.title('Metoda sečen');
Algoritmus metody sečen
Implementujte metodu sečen doplněním následujícího kódu. Je možné, že metoda nebude konvergovat! Pak je potřeba změnit počáteční interval. Pro jaké hodnoty \(a_0\) a \(b_0\) metoda konverguje?
Do pole reseni2 uložte vždy řešení a do pole epsilon2 odpovídající chybu v každé iteraci.
eps2 = 1e-15
iteraci_max2 = 100
a = 0.1 # ZKUSIT -6, 0.1
a1 = 5
# budeme si prubezne ukladat odhad reseni a chybu odhadu
epsilon2 = np.ones(iteraci_max2) # odhad relativni chyby, tedy delku intervalu <a,b> v jednotlivych krocich
reseni2 = np.zeros(iteraci_max2) # aktualni odhad reseni
i = 0
## DOPLŇTE ##
iteraci_end2 = i
koren2 = reseni2[i-1] # odhad konecneho reseni
chyba2 = epsilon2[i-1] # odhad konecne chyby
print(koren2, iteraci_end2, chyba2)
-4.282289017870752 14 8.29629589216047e-16
Porovnání s metodou bisekce:
print('Bisekce:', koren, f(koren), chyba) # predchozi vysledek
print('Sečna: ', koren2, f(koren2), chyba2)
Bisekce: -4.2822890178707524 -2.1316282072803006e-14 5.185184932600293e-16
Sečna: -4.282289017870752 7.105427357601002e-15 8.29629589216047e-16
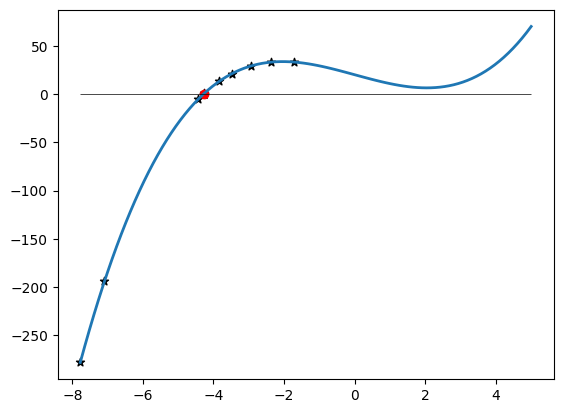
# vykresleni reseni
xmin = np.min([-6, np.min(reseni2[:iteraci_end2])])
xmax = np.max([5, np.max(reseni2[:iteraci_end2])])
x = np.linspace(xmin, xmax, 100)
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=xmin, xmax=xmax)
plt.scatter(reseni2[:iteraci_end2], f(reseni2[:iteraci_end2]), c='k', marker='*')
plt.scatter(koren2, f(koren2), c='r');
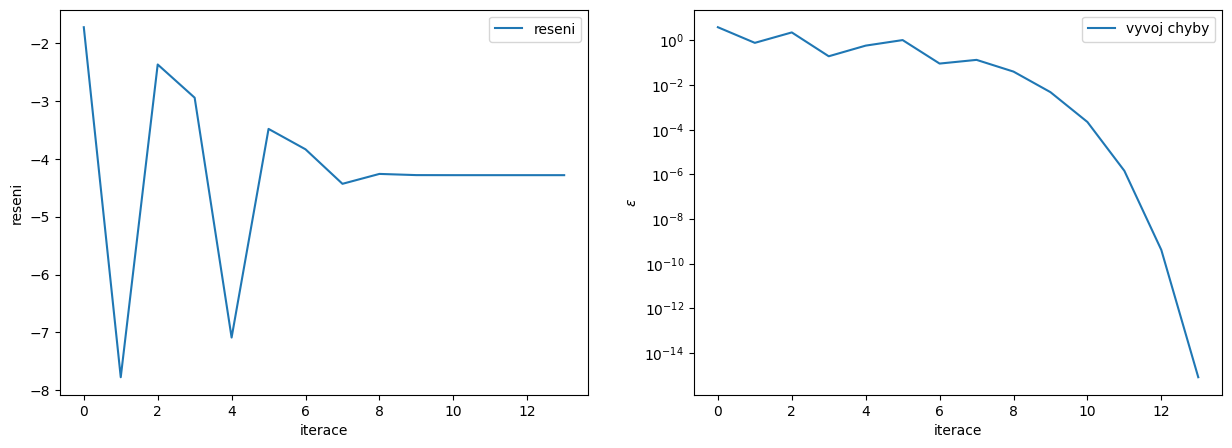
fig, ax = plt.subplots(1,2,figsize=(15,5))
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci_end2),reseni2[:iteraci_end2],label='reseni')
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci_end2),epsilon2[:iteraci_end2],label='vyvoj chyby')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
ax[1].set_yscale('log')
ax[1].legend();
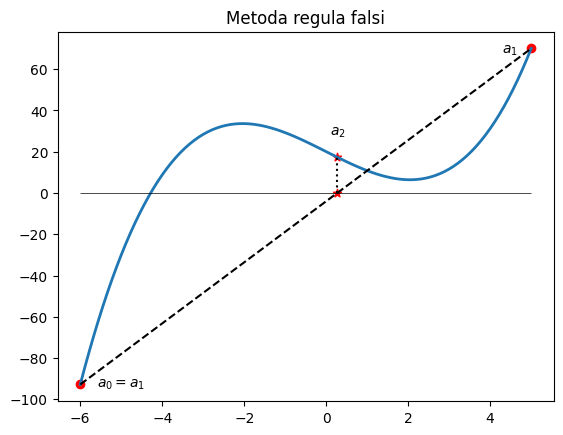
Metoda regula falsi#
modifikace Metody sečen
po určení \(a_{n+1}\) si k němu vyberu z \(a_{n-1}\) a \(a_{n}\) takový bod \(a_{n}\), aby kořen zůstal ohraničený, tj. \(f(a_{n})f(a_{n+1})<0\)
konvergence je zaručena
# vykresleni funkce
x = np.linspace(-6, 5, 100)
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=-6, xmax=5)
plt.scatter([a0, b0], [f(a0), f(b0)], c='r')
# vizualizace kroku
c = (a0*f(b0)-f(a0)*b0)/(f(b0)-f(a0))
plt.plot([a0, b0], [f(a0), f(b0)], 'k--')
plt.plot([c, c], [0, f(c)], 'k:')
plt.scatter([c, c], [0, f(c)], c='r', marker='*')
plt.text(4.3,68,'$a_1$')
plt.text(-5.6,-94,'$a_0 = a_1$')
plt.text(0.1,28,'$a_2$')
plt.title('Metoda regula falsi');
Algoritmus metody regula falsi
Implementujte metodu regula falsi doplněním následujícího kódu. Tentokrát metoda bude konvergovat.
Do pole reseni3 uložte vždy řešení a do pole epsilon3 odpovídající chybu v každé iteraci.
eps3 = 1e-15
iteraci_max3 = 100
a = -6
a1 = 5
# budeme si prubezne ukladat odhad reseni a chybu odhadu
epsilon3 = np.ones(iteraci_max3) # odhad relativni chyby, tedy delku intervalu <a,b> v jednotlivych krocich
reseni3 = np.zeros(iteraci_max3) # aktualni odhad reseni
i = 0
## DOPLŇTE ##
iteraci_end3 = i
koren3 = reseni3[i-1] # odhad konecneho reseni
chyba3 = epsilon3[i-1] # odhad konecne chyby
print(koren3, iteraci_end3, chyba3)
-4.282289017870751 39 6.222221919120353e-16
Srovnání výsledků různých metod:
print('Bisekce: ', koren, f(koren), chyba, iteraci_end) # predchozi vysledek
print('Sečna: ', koren2, f(koren2), chyba2, iteraci_end2)
print('Regula-falsi:', koren3, f(koren3), chyba3, iteraci_end3)
Bisekce: -4.2822890178707524 -2.1316282072803006e-14 5.185184932600293e-16 51
Sečna: -4.282289017870752 7.105427357601002e-15 8.29629589216047e-16 14
Regula-falsi: -4.282289017870751 3.552713678800501e-14 6.222221919120353e-16 39
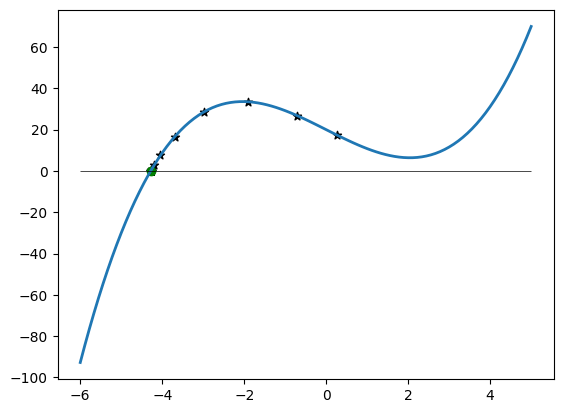
# vykresleni reseni
x = np.linspace(-6, 5, 100)
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=-6, xmax=5)
plt.scatter(reseni3[:iteraci_end3], f(reseni3[:iteraci_end3]), c='k', marker='*')
plt.scatter(koren3, f(koren3), c='g');
fig, ax = plt.subplots(1,2,figsize=(15,5))
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci_end3),reseni3[:iteraci_end3],label='reseni')
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci_end3),epsilon3[:iteraci_end3],label='vyvoj chyby')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
ax[1].set_yscale('log')
ax[1].legend();
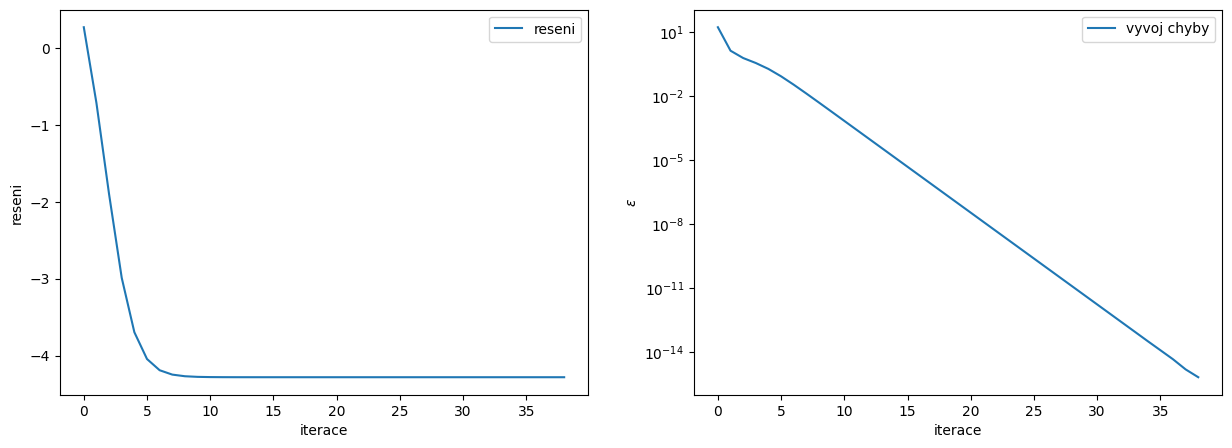
Newton–Raphsonova (tečnová) metoda#
využívá první derivaci zadané funkce (je vhodná, pokud umíme hodnoty derivací rychle počítat)
Taylorův rozvoj zadané funkce v okolí bodu \(x_{i}\): \( f(x_{i}+\Delta x)=f(x_{i})+\Delta x f'(x_{i})+\dfrac{(\Delta x)^{2}}{2}f''(x_{i})+\dots \)
vypočítáme \(\Delta x = x_{i+1} - x_{i}\) z podmínky \(f(x)=0\)
iterační vzorec: \(x_{i+1}=x_{i}-\dfrac{f(x_{i})}{f'(x_{i})}\)
konvergence není zaručena
def f(x):
return 0.8 * x**3 - 10*x + 20
# analyticky určená derivace
def dxf(x):
return 2.4 * x**2 - 10
# numericky - pomocí konečné diference
def dxf2(x, h):
return (f(x+h) - f(x)) / h
a0 = -3 # volba pocatecniho bodu, ZKUSIT -3, 2.2, 2, 10
a1 = a0 - f(a0) / dxf2(a0, 0.01)
# vykresleni funkce
x = np.linspace(np.min([-6, a1]), np.max([5, a1]), 100)
tecna = f(a0) + dxf(a0) * (x - a0) # funkce tecny v bode a0
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=np.min([-6, a1]), xmax=np.max([5, a1]))
plt.scatter([a0], [f(a0)], c='r')
# vizualizace kroku
plt.scatter([a1, a1], [0, f(a1)], c='r', marker='*')
plt.plot(x, tecna, 'k--')
plt.plot([a1, a1], [0, f(a1)], 'k:')
plt.text(a0*0.95,f(a0)*0.75,'$a_0$')
plt.text(a1*0.95,f(a1)*1.1,'$a_1$')
plt.title('Metoda Newton-Raphson');
Algoritmus Newton–Raphsonovy metody
Implementujte Newton–Raphsonovu metodu doplněním následujícího kódu. Je třeba vhodně zvolit počáteční odhad, aby metoda konvergovala! Pro jaké počáteční hodnoty metoda konverguje? Pro které ne?
eps4 = 1e-15
iteraci_max4 = 100
a0 = -3 # ZKUSIT -3, 2.2, 2, 10
# budeme si prubezne ukladat odhad reseni a chybu odhadu
epsilon4 = np.ones(iteraci_max4) # odhad relativni chyby, tedy delku intervalu <a,b> v jednotlivych krocich
reseni4 = np.zeros(iteraci_max4) # aktualni odhad reseni
i = 0
## DOPLŇTE ##
iteraci_end4 = i
koren4 = reseni4[i-1] # odhad konecneho reseni
chyba4 = epsilon4[i-1] # odhad konecne chyby
print(koren4, iteraci_end4, chyba4)
-4.282289017870752 10 0.0
Porovnání s výsledkem funkce fsolve() z knihovny SciPy:
koren_SP2 = fsolve(f, a0)
Srovnání výsledků různých metod:
print('Bisekce: ', koren, f(koren), chyba) # predchozi vysledek
print('Sečna: ', koren2, f(koren2), chyba2)
print('Regula-falsi: ', koren3, f(koren3), chyba3)
print('Newton-Raphon:', koren4, f(koren4), chyba4)
print('fsolve(): ', koren_SP2, f(koren_SP2))
Bisekce: -4.2822890178707524 -2.1316282072803006e-14 5.185184932600293e-16
Sečna: -4.282289017870752 7.105427357601002e-15 8.29629589216047e-16
Regula-falsi: -4.282289017870751 3.552713678800501e-14 6.222221919120353e-16
Newton-Raphon: -4.282289017870752 7.105427357601002e-15 0.0
fsolve(): [-4.28228902] [7.10542736e-15]
# vykresleni reseni
xmin = np.min([-6, np.min(reseni4[:iteraci_end4])])
xmax = np.max([5, np.max(reseni4[:iteraci_end4])])
x = np.linspace(xmin, xmax, 100)
plt.plot(x, f(x), linewidth=2)
plt.hlines([0], colors=['k'], linewidths=[0.5], linestyles=['-'], xmin=xmin, xmax=xmax)
plt.scatter(reseni4[:iteraci_end4], f(reseni4[:iteraci_end4]), c='k', marker='*')
plt.scatter(koren4, f(koren4), c='r');
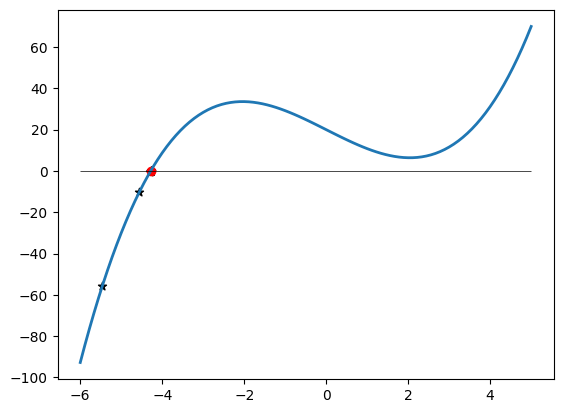
fig, ax = plt.subplots(1,2,figsize=(15,5))
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci_end4),reseni4[:iteraci_end4],label='reseni')
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci_end4),epsilon4[:iteraci_end4],label='vyvoj chyby')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
ax[1].set_yscale('log')
ax[1].legend();
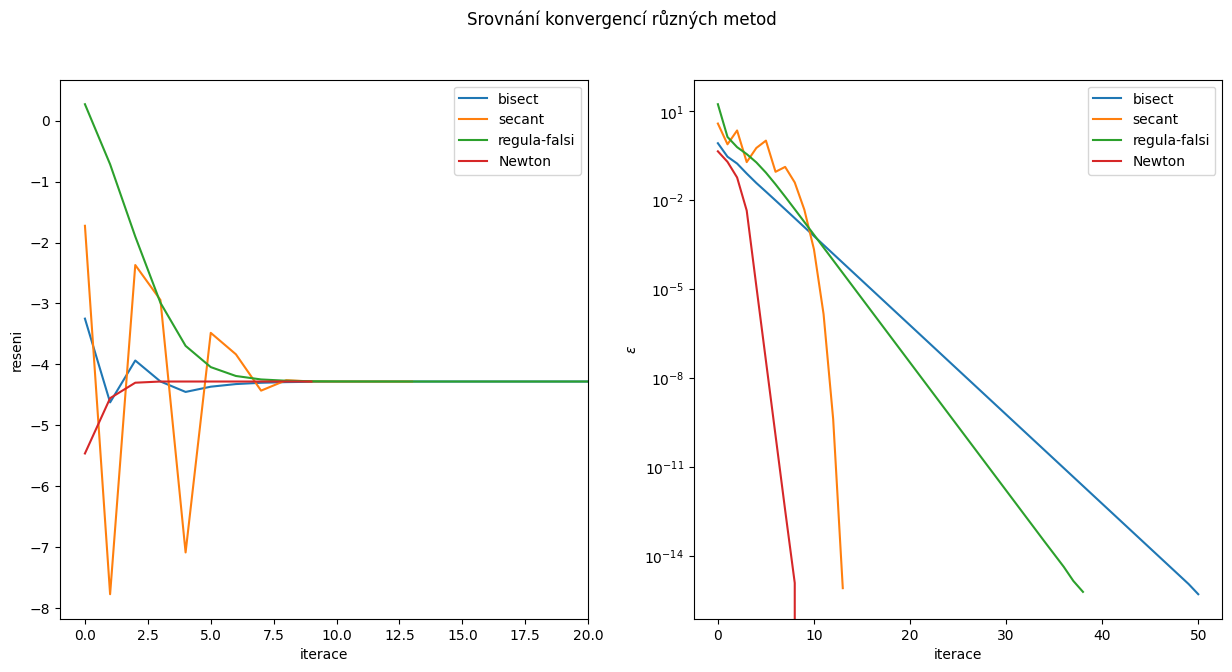
Srovnání konvergencí#
fig, ax = plt.subplots(1,2,figsize=(15,7))
fig.suptitle('Srovnání konvergencí různých metod')
# zobrazime vyvoj reseni v zavislosti na iteracich
ax[0].plot(range(iteraci_end),reseni[:iteraci_end],label='bisect')
ax[0].plot(range(iteraci_end2),reseni2[:iteraci_end2],label='secant')
ax[0].plot(range(iteraci_end3),reseni3[:iteraci_end3],label='regula-falsi')
ax[0].plot(range(iteraci_end4),reseni4[:iteraci_end4],label='Newton')
ax[0].set_xlim([-1, 20])
ax[0].set_ylabel('reseni')
ax[0].set_xlabel('iterace')
ax[0].legend()
# zobrazime vyvoj chyby v zavislosti na iteracich
ax[1].plot(range(iteraci_end),epsilon[:iteraci_end],label='bisect')
ax[1].plot(range(iteraci_end2),epsilon2[:iteraci_end2],label='secant')
ax[1].plot(range(iteraci_end3),epsilon3[:iteraci_end3],label='regula-falsi')
ax[1].plot(range(iteraci_end4),epsilon4[:iteraci_end4],label='Newton')
ax[1].set_yscale('log')
ax[1].set_ylabel(r'$\epsilon$')
ax[1].set_xlabel('iterace')
ax[1].legend();
Soustavy nelineárních rovnic#
řešíme soustavu \(\vec{f}(\vec{x})=\vec{0}\)
přepíšeme ji do tvaru:
Newton-Raphsonova metoda 2D#
přesné řešení \(\vec{\xi}\) vyjádříme ve tvaru \(\vec{\xi}=\vec{x}+\delta\vec{x}\)
hodnotu funkce v bodě \(\vec{\xi}\) vyjádříme pomocí Taylorovy věty: \( f_{i}(\vec{x}+\delta\vec{x})=f_{i}(\vec{x})+\sum_{j=1}^{n}\dfrac{\partial f_{i}}{\partial x_{j}}\delta x_{j}+\mathcal{O}(\delta \vec{x}^{2}) \)
zanedbáním \(\mathcal{O}(\delta \vec{x}^{2})\) získáme: \( f_{i}(\vec{x}+\delta\vec{x})=f_{i}(\vec{x})+\sum_{j=1}^{n}\dfrac{\partial f_{i}}{\partial x_{j}}\delta x_{j}=0 \)
řešíme tedy soustavu \(n\) lineárních rovnic s neznámou \(\delta \vec{x}\), označme \(\mathbb{J}_{i,j} = \dfrac{\partial f_{i}}{\partial x_{j}}\)
dostaneme soustavu: \(\mathbb{J} \cdot \delta \vec{x} = -\vec{f}\)
iterační vztah pro funkci \(n\) proměnných: \(x_{i}^{(k+1)}=x_{i}^{(k)} - \sum_{j=1}^{n}\mathbb{J}_{i,j}^{-1} f_{j}\)



